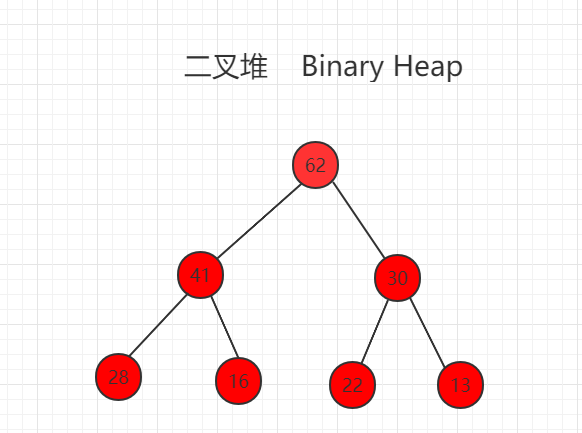
【算法】堆和堆排序
📲堆
🏒概念
以下源自百度百科对堆的解释说明。
堆(heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做
一棵树的数组对象。堆总是满足下列性质:
堆中某个结点的值总是不大于或不小于其父结点的值;
堆总是一棵完全二叉树。
将根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
堆是非线性数据结构,相当于一维数组,有两个直接后继。
若将和此次序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{k1,k2,…,kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
(以上源自百度百科)
堆的定义如下:n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆。
这种则被称为小堆,其父节点小于他的两个子节点。
反之则被称为大堆。
因为堆的逻辑结构是一棵完全二叉树,所以虽然用数组的形式来存,但我们思考其实现要考虑以树的结构来做。这里的下标用到了二叉树的知识点,当一个节点为i时,其左右子节点(存在的话)为2 * i+1与2 * i+2,请注意下标从0开始计算。
堆的实现多种多样,本文给出一种简单可行的建堆方式。
🏸初始化堆
首先是实现堆的初始化。
但在实现堆的初始化要对其结构进行定义。
这里给出的是以动态开辟内存的数组来实现的,定义arr作为数组开始的基址,capacity为总的容量,size为当前的容量,二者一起控制整个数组的大小。
1 | typedef struct heap{ |
书写初始化函数。
1 | void heapinit(heap* hp) { |
为arr申请四个int的空间来存放数据,同时将capacity置为4,sizie置0,没什么特别需要解释的地方。
🥋往堆中放入数据
下一步就是书写push的函数。插入数据没什么难的,难点在于插入这个数据后,堆是否还是个堆。例如刚开始没有数据,一个数据就是一个堆,那插入第二个数据,就要基于建大小堆考虑调整方案。
1 | void heapinit(heap* hp) { |
🤸♀向上调整算法
重点要讲的就是堆调整的算法—向上调整算法。
以上图为例,我们建立一个大堆,那么向上调整的意思就是从最后一个节点开始,与自己的父节点进行比较,如果比父节点大,就将值和父节点进行交换,然后从下往上遍历这个分支。
1 | void adjustup(int* arr, int child){ |
父节点和子节点的关系在开头就已经提出过,在此就不多赘述。 但请让在插入整个数据前,前面的数据已经是一个堆了。
以上一个图为例,因为是插入一个数据就调整一次,当插入到最后的60时,前面就已经是大堆了。所以我们只需要沿着60这个分支往上进行遍历。
🤸♂向下调整算法
如果不是单个数据的插入,而是直接给出一个数组让你将他调整为堆,可以使用向下调整算法。又或者你将堆中一个数据进行了删除,也得使用向下调整来调整整个结构。
使用这个算法有前提:
若想将其调整为小堆,那么根结点的左右子树必须都为小堆。
若想将其调整为大堆,那么根结点的左右子树必须都为大堆。
1 | void adjustdown(int* arr, int parent,int n) { |
这里加入的参数比向上调整多了一个n,n在这里代表传入的数据长度,用来判断孩子是否越界的。
🥅堆删除(pop)
先给出一个判断堆是否为空的函数,方便后面进行断言
1 | bool heapempty(heap* hp) |
pop函数
1 | void heappop(heap* hp) { |
将弹出的数据与最后一个下标交换,然后使用向下调整即可。
🏏topk问题
topk问题的本质就是筛选出一组数据中最大或最小的前k个。
虽然排序可以解决,但是一旦数据量大起来,比如100亿个数据,就无法全部加载到内存来进行排序,而且耗费的时间也很大,例如选最大的k个数,我们采取先将前k个数据建立一个小堆,再遍历剩下的数据,如果遇到比堆顶大的数据,就将其进行入堆并且向下调整。选取最小的k个数,则建立一个大堆。
我们以选取前k个最大值为例,进行代码书写:
1.建堆
2.遍历剩下的数据,比堆顶大则入堆替换,并向下调整。
代码如下:
1 | void printtopk(char* file, int k) |
int i = (k - 2) / 2这里需要解释以下,因为k在这里代表的是数据个数,然而数组的小标从0开始,所以要额外减一个1。
当然建堆也可以使用向上调整,那么从下标1开始即可,因为第一个也没必要去调。
1 | for (int i = 1; i < k; ++i) |
然后就只需要将剩下的数据挨个进行读取,然后与堆顶进行比较即可,比堆顶大则代替堆顶,并向下调整。
🏄堆排序与其时间复杂度
堆排序有了topk问题的铺垫,就很简单了,首先仍然是建堆。
1 | // 建堆 -- 向上调整建堆 -- O(N*logN) |
那么此时出现了问题,如果我们需要的是一个升序序列,那应该建大堆还是小堆呢?
答案是大堆。如果建的是小堆,确实可以筛选出最小的那个数,就在堆顶,很方便,但是当你取走了堆顶,就会造成关系的混乱,小根堆的性质就已经变了,此时可能出现儿子变成爹的情况,此时就需要重新调整整个结构,得不偿失。如果建立的是大堆,每次向下调整都可以得到剩余的数据最大值。只需要将每次调整得到的最大值从后往前放即可。
这要和topk问题分清楚哦。
所以剩余的代码如下:
1 | int end = n - 1; |
堆排序是一种非常快速的排序,其时间复杂度为O(n*logn)。
以向下调整为例,是从最后一层开始调的:
高度从1开始,假设为一个满二叉树。
建堆时,每一个数都会与下面的层数进行对比,满足条件即交换,最多的情况下就会交换h-n次,n为当前的层数。
可见建堆的比较次数为:
这是一个等比等差的数列,使用高中的知识,可以将t*2,再将两式相减,即可得出:
又因为这是满二叉树,即,所以
那么就可以近似认为复杂度为O(n)了。
向上调整也是同理,从第一层开始调整:
仍然是错位相减,可以得到:
也就是n*logn了。
为何向上要比向下更复杂呢?因为向上用到了最后一层,最后一层相当于有接近总数一半的节点!
建堆的复杂度分析完毕,接下来就是排序的部分了。
只看最后一层,都有个节点,最坏情况下,每个都要比较h-1次,也就是
这里就很想向上调整了:
所以得到排序的复杂度也是o(n*logn)了。